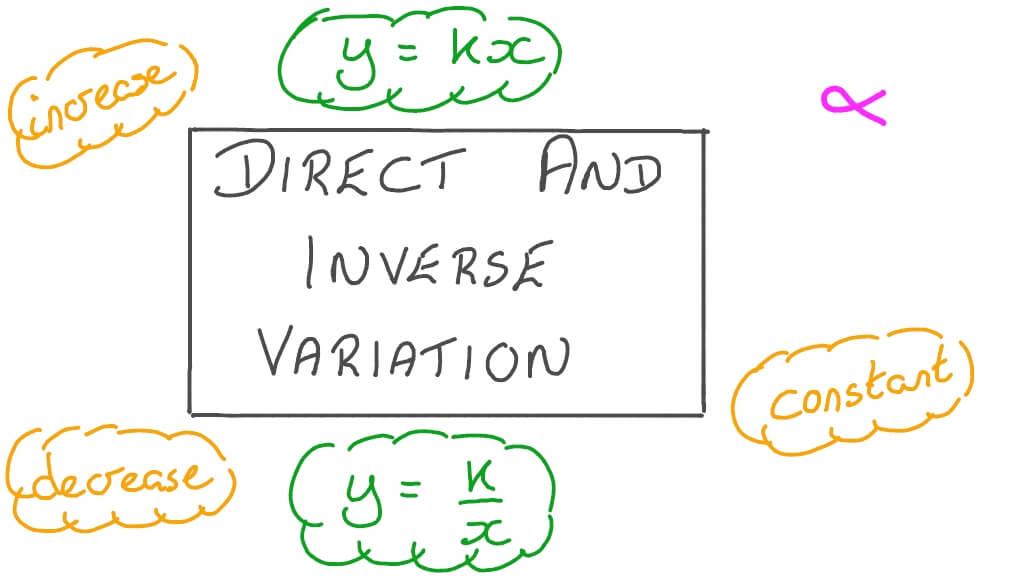
An inverse variation is a kind of relationship where one value increases while the other one decreases.
For example, if one quantity increases while the other decreases, the quantities can have an inverse relationship.
Inverse variation is the opposite of direct variation, where there is a linear relationship between two variables.
An inverse variation relationship can be represented by this equation:
xy=k or y=k/x
where x and y are the variables and k is a constant value.
In the above equation, if x increases, y decreases and if x decreases, y will increase. K is a constant, so it will always remain the same throughout the inverse variation problem.
Let’s explore examples of inverse variation in real life.
1. Speed and Time when Heading to a Particular Location

If you are heading to a particular location, the time taken to reach a particular destination decreases as you increase your speed.
On the other hand, if you decrease the speed, you increase the time you would take to reach the destination.
Therefore, speed is inversely proportional to time in this case. However, you must have a fixed distance for the relationship to work.
2. Sunlight in the Solar System

The brightness of a light is dependent on the distance between the source and the person viewing it.
This happens with light in the solar system. The distance between the sun and the planet determines the brightness of the sunlight from a viewer standing on the planet.
It increases as you come closer to the sun and decreases when you go further.
Someone on Pluto will see a flicker of light and gets better as one moves back to earth.
3. The Number of Cars and Space in the Parking Lot

There is a definite number of parking slots in any yard. The number of spaces in the parking lot increases or decreases with the number of vehicles that are parked.
If you decrease the number of vehicles, the space in the parking lot increases.
However, if you increase the number of cars, the number of slots goes down.
So, the number of cars is inversely proportional to the parking slots.
4. The Length of Violin String with the Frequency of Vibrations

The length of a violin string is inversely proportional to the frequency of its vibrations.
The longer the violin string, the lower the frequency of its vibrations.
Tightening the string helps in shortening the length to increase the frequency of vibrations.
The increase or decrease in frequency helps enhance the pitch of the sound. This principle is applied to all other string instruments.
5. Time to Finish Work and the Number of Workers

The time to finish a particular task decreases if you increase the number of workers.
For example, if one person can move 50 crates of soda in 5 hours, it would take five people working at the same rate an hour.
In this case, the number of hours it takes to complete a task is inversely proportional to the number of workers on a job.
6. Cows Grazing in a Field

If you have cows grazing in a piece of land, the length of time they take to finish the pasture depends on the number of cows in the paddock.
If you increase the number of cows in a paddock, the time it takes to finish off the pasture goes down, and vice versa is true.
Therefore, time is inversely proportional to the number of cattle.
7. A tap Draining Water from A tank

If a tap drains some water from a tank to a container, the amount of water in the tank goes down while that of the container goes up.
If you continue draining the water from the tank, the tank will be dry after a time while the said container will get filled up.
So, the draining of the tank is inversely proportional to the amount that gets into the container.
8. Quality and Use of a Tire

The quality of a car’s tire is inversely proportional to its use.
If you use the vehicle regularly, the tire will degrade rapidly, thereby making it poor.
On the other hand, if you use the car a few times, you can retain the quality of your tire for long.
In this case, the quality is inversely proportional to the use.
9. Food Consumption and Amount of Food

The amount of food that is available is inversely proportional to the consumption of the same.
If you have ten plates of French fries and five are eaten, the number decreases to five.
On the other hand, the consumption rate rises from zero to five.
Farmers look at the consumption rate of different animals when determining the number of bags of feeds to buy.
10. Power Consumption and Units Consumption

If you have a standard number of units for usage in running equipment, the number of hours you consume power reduces the number of available units.
Therefore, if you plot a graph on consumption and the number of available units, the consumption rate would go up while that of the available units goes down.
This principle is used to budget for power consumption.
Parting Thoughts
There you have it—10 examples of inverse variation in real life. Essentially, if any action or events decrease when you increase any other variable, the two are inversely proportional to each other. Look for other examples around home and workplace.
Related Posts:
Related Posts: