To answer the question, you need to understand the difference between linear pairs and supplementary angles:
Linear Pairs
Linearity is the dominant principle used in geometric calculations.
It represents all that is within a straight line; the shortest path from one point to another.
Lines also form a straight angle of 180 degrees.
This implies that all adjacent angles at any point of a line should add up to 180 degrees.
As such, one of the many conjectures used in geometry is the concept of linear pairs of angles.
These are angles that are adjacent to each other, on a straight line. Such pairs are always formed by intersecting two straight lines.
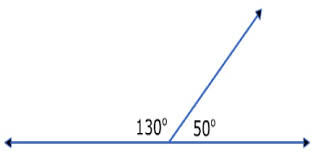
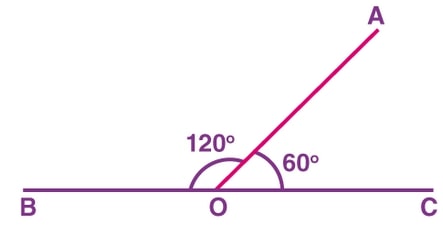
Case in point, as shown in figure 1 below, line BC forms a straight angle of 180 degrees.
Therefore, at point O, lines BC and AO intersect to form two adjacent angles that add up to 180 degrees.
This is a linear pair of angles given that they are adjoining on a straight line and they add up to 180 degrees.
Supplementary Angles
On the other hand, supplementary angles are those that total up to 180 degrees.
The term ‘supplementary’ is used to describe items that act in a supporting capacity for each other.
As such, supplementary angles come together to form a straight-line angle.
It should be noted, however, that supplementary angles are not always adjacent to each other.
Adjacent supplementary angles are on a straight line while non-adjacent supplementary angles do not share a vertex or an arm.
Vertex refers to the point at which two or more lines intersect to form an angle.
Arms are the lines that connect to form an angle.
Neither are non-adjacent supplementary angles formed using the same arms nor do they occur at the same vertex.
Nonetheless, these kinds of angles always add up to 180 degrees.
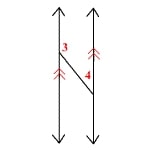
For instance, in figure 2 below, angles 3 and 4 are supplementary being that they add up to 180 degrees.
They are formed by one arm that cuts across two parallel lines, creating a straight-line angle.
However, these angles are non-adjacent as they do not share a vertex.
So, Are All Supplementary Angles Linear Pairs?
No, supplementary angles are not always linear pairs.
However, all linear pairs are supplementary angles.
This is to mean that linear pairs always sum up to 180 degrees, making them supplementary.
In contrast, supplementary angles are not always adjacent to each other.
All adjacent supplementary angles are linear pairs since they are formed at one point on a straight line.
Conversely, non-adjacent supplementary angles are not linear pairs given that they are not positioned at the same vertex.
For instance, as detailed in figure 2, angles 4 and 3 are supplementary but not linear.
Conclusion
In summary, linearity is the primary attribute of linear pairs.
A linear pair of angles comprises supplementary angles that occur at the same vertex and are adjacent to each other.
Therefore, all linear pairs are supplementary angles.
On the flip side, not all supplementary angles are linear pairs.
Non-adjacent supplementary angles are an exception as they do not adjoin each other.