DEFINITIONS:
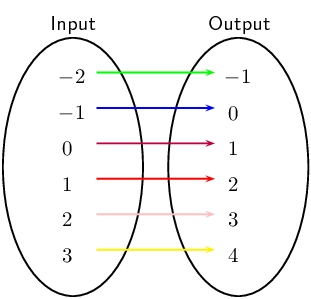
Functions are mathematical relationships where each input (from a set called the domain) corresponds to exactly one output (from a set called the range), while relations allow multiple outputs for an input.
EXPLANATION:
Relations are defined as sets of ordered pairs. Ordered pairs are values that go together. This means that if one value is used, the other must be present.
Here is an example: If (4,8) is an ordered pair, then it implies that if the first element is 4 the other is designated as 8. A relation may have more than one output.
On the other hand, a function is a relation where one x-element (or the output) has one Y-element (or the input associated with it).
In ordered pairs, a relation becomes a function if the x-value is not repeated.
If the values were to be plotted on a graph, a relation could become a function if no vertical lines intersect at any point in the graph.
EXAMPLES
Here are real-life examples of relations and functions.
1. The Relationship between Age and Height

If you took a group of people at random, you would notice a relationship between their ages and height. This is because people get taller with time and then remain at the same height for a while.
This is a relation because if you input a specific age and check all the people of that age, you would get different heights.
However, if you were to take the height of a particular person over the years, the height would be a function of age. This is because a person would have only one value of height at any point in life.
2. A Semester in School

In a college, students take different classes to fulfill the requirements of a given course.
A student may have different grades for different subjects. Therefore, there is a relation between the student and his grades.
However, in a single class, the tutor assigns each student a grade depending on the performance of that particular subject. There can never be a student with two grades in a single subject.
3. Temperature and Location

A location may have varying temperatures according to the time of the day and weather. This may repeat itself over the years as long as the conditions are similar to those of the last time. That can be said to be a relation.
However, the temperature can also be a function of time. At any one time, there can only be one temperature reading for a location.
4. The Cost of Fuel

Once you pull over to a gas station, the cost of filling your car is dependent on the amount of gasoline you put into its tank.
Therefore, the cost is a function of the quantity in this case. There can never be two costs for the same quantity of fuel in a gas station.
Most people estimate the amount of fuel to put into their vehicle based on the cost of a liter of gasoline.
5. The Cost of Taking a Taxi

Taxis estimate the cost of your ride based on the amount of time you spend on their vehicle.
Many of them have a counter that starts when a rider enters the vehicle.
Therefore, the cost of a particular ride is the function of how long your ride is. You cannot have two charges for the same duration.
6. Money Won from a Lottery Ticket

The cash won from buying a lottery scratchcard may differ for two or more tickets. Therefore, you cannot say for sure how much you are likely to make by scratching several tickets.
Besides, a single ticket may be eligible for more than one draw where it loses both, wins one, or both. This is a classic example of a relation.
7. The Number of Sodas in a Vending Machine

The number of sodas you get from a vending machine depends on how much money you feed into the machine.
If you put the same amount twice and pick the same soda, you will get a similar number of cans as you got in the first place.
In this case, the number is a function of the amount you feed into the machine.
8. Places you can drive with Two Gallons of Fuel

If you have two gallons of fuel left in your car’s fuel tank, you can visit several places before running out of gas. Therefore, there can be several answers to this question.
In this case, the input is the two gallons of fuel, while the output is the names of places you can visit with this much fuel.
9. The Velocity of an Object in Free Fall

In physics, a free-fall object accelerates at 10m/s2 if you exclude the air resistance.
There can only be one particular speed at any point in time as the object falls to the ground.
Therefore, speed, in this case, is a function of the number of seconds that the object has been in free fall.
10. An ATM Machine

If you would like to withdraw cash from your account, the amount of cash dispensed by the machine is equal to the amount you request.
Therefore, the amount requested is the function of the amount dispersed. The machine can never give you more or less than what you have requested.
Conclusion
There you have it; 10 examples of functions and relations in real life.
Any action that depends on input is either a relation or a function.
The difference between the two is the number of outcomes that may come from the single input.
Related Posts: Applications of Rational Functions in Real Life