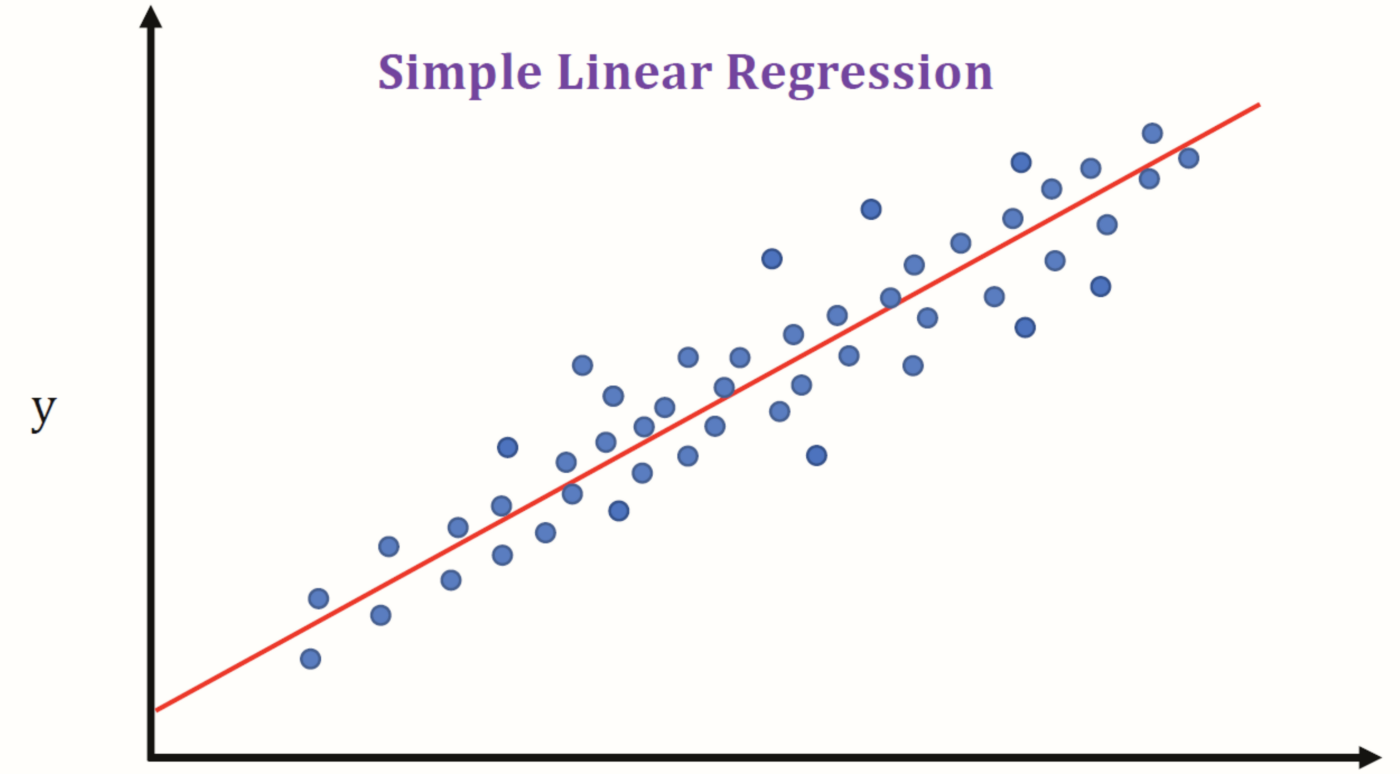
Linear regression is a statistical method to model the relationship between two variables, utilizing a linear equation to predict the value of one variable based on the other’s values.
How can you know if there is any connection between the variables in your dataset?
Statisticians usually turn to a tool called linear regression. This involves a process that enables you to identify specific trends in your data.
In linear regression, there is always an independent variable and a dependent variable.
We use the independent variable as the predictor variable or the explanatory variable. This is what explains the phenomenon you are studying.
The dependent or response variable is produced whenever you vary your predictor variable.
So, as you adjust your independent variable, your dependent variable should respond too if there is a real association between them.
Depending on the nature of the relationship between the variables in your dataset, you can get any of these three outcomes
- Positive Relationship: When the independent variable x increases (which happens on the x-axis), the dependent variable y also increases (which happens on the y axis)
- Negative Relationship: When the independent variable x increases (which happens in the x-axis), the dependent variable y decreases (which happens on the y axis)
- No Relationship: This shows no changes to link the dependent and the independent variable
Types of Linear Regression
Linear regression can either be simple or complex.
- Simple: This studies the relationship between 2 variables
- Complex: This looks at the relationship between more than one variable
A linear regression model will generate a straight line with a slope that tells you the relationship between the variables.
To do this, a statistician produces a scatter plot which is a graph in which all the data points are plotted.
Then he will draw a best fit line that tries to connect the data points with the least error.
This best fit line is also called a regression line and it will be strongly suggested only if there is a strong correlation between the variables.
Regression can be very useful in uncovering hidden links between variables and also to obtain a predictive model.
Here are 12 examples of linear regression in real life
1. Risk Assessment For Insurance

An insurance company may rely on linear regression to know what to charge for their premiums.
It can use various factors such as characteristics of your car, population information, to construct a premium table that contains information comparing predicted claims with a declared value of the insured car
2. The Impact Of A Supplement On Weight Loss

If an overweight person is taking weight loss supplements, you can study whether there’s any connection between them.
The supplement is considered as the independent variable while weight is the dependent variable. This can help you to judge the efficacy of the supplement.
3. Gauging The Impact Of Advertising On Sales

Is there any use for advertising as a way of driving your sales?
If so, how can you predict the effect of a given amount of advertising budget?
You can confirm this by looking at the advertising expense and your sales over time.
In this data, your advertising cost acts as the independent variable, and your sales are the response variable.
4. Economic studies
Linear Regression is widely used in economics for analysis.
Economists want to predict various factors like fixed investment spending, consumer spending, imports, exports, demand, and supply.
Linear regression helps to reveal insights into these and more.
5. Predicting Growth From Food Nutrients Eaten

As a biologist, you may want to find out if there is any connection between a particular nutrient that an animal eats and how much it grows.
By collecting data each day for the food taken and weight changes, you can create a predictive model for associating these two variables and knowing the nutritive value of the food.
6. The amount of water vs the height of a plant

Watering a plant is believed to lead to an increase in growth of a plant.
We can investigate this by collecting data on the water applied every day and the changes in the height of the plant.
7. Machine learning

Linear regression is an important tool used to help machines learn and to develop artificial intelligence (AI) capabilities such as in self-driving cars or playing against human players at difficult games.
This is done through a technique called supervised learning that helps to find the correlation between variables through a learning algorithm.
This learning process helps the machine improve and get and better at doing tasks
8. Finding the connection between cool drink sales and temperature

If you are running a refreshment business, you may eat to know how well the weather correlates with the number of drink sales you make.
9. The linear connection between water bill and amount of water used

The amount of water used is the explanatory variable while the billings is the response variable.
This may indicate whether there are water leaks in your system for which no one is paying.
10. The connection between carbon emissions and average temperature

There has been much contention between whether carbon emissions have any relationship with climate change (specifically global warming).
This can be studied by data of annual carbon emissions and the annual average temperature levels of each year.
If you can establish a connection, you can also predict how dire the situation will be in the coming years
11. Work experience vs salary

You can use company data to relate salaries paid to employees and their years of experience.
The independent variable is the years worked while salaries are the independent variable.
12. The connection between meat consumption and obesity

Does meat consumption lead to cancer? We can gather data on this treating meat consumption as the independent variable and cancer incidence as the dependent variable.
Conclusion
Linear regression is a tool for unearthing previously unrecognized patterns and relationships between variables.
They are useful for making estimates and predictions which can be the basis for decision making.