Transversals are one of the best ways of gaining insights into the principles of geometry and angles.
These principles are also useful for practical purposes such as when building structures.
However, before we get into them, let’s first understand a few basics…
What are parallel lines?
Parallel lines in geometry are two or more straight lines in the same plane that never intersect, maintaining a consistent, equidistant relationship throughout their length, denoting no meeting point.
When two lines never cross each other, we call them parallel lines.
These lines will never intersect each other, however much we extend them to infinity.
This also means that any line that lies perpendicular to either line will also be perpendicular to the other line.
The distance separating them will also always remain a constant.
An example is the opposite walls of a room.
What do we mean by coplanar?
Coplanar means lying on the same plane or flat surface. An example is two points drawn on the same sheet of paper with the paper representing a plane.
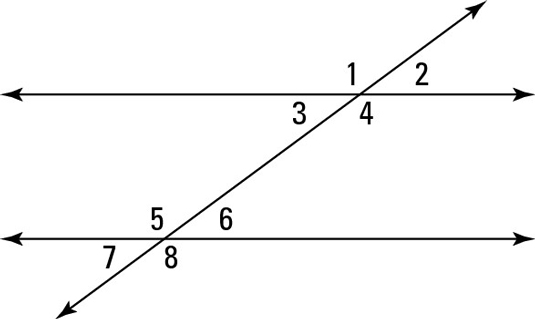
Transversals
When a line cuts two coplanar lines, we refer to it as a transverse line or a transversal.
The transversal can either cut the parallel lines diagonally or at perpendicular angles.
Properties of transversals
When transverse lines are created, they produce a range of key angle relationships such as the following:
- Corresponding angles which are always congruent. These angles have corresponding locations which make them equal.
- Same side interior angles which are supplementary—add up to 180 degrees. These angles are found inside the lines which share the same side with the transversal.
- Alternate interior angles which are always congruent. These angles are located inside the line but lie opposite sides to the transversal.
- Alternate exterior angles which are always congruent.
Here are 9 examples of parallels lines cut by transversals:
1. Railway with sleepers

Railway tracks are usually constructed with horizontal supports underneath the rails called sleepers.
Their function is to secure the rail so that they won’t shift under the heavy force of the moving trains.
They form a transverse alignment with the rail which is essential for offering secure support.
2. Car Windscreen wiper

As the wipers move on the windscreen, they continuously alter their angle to the edges of the windscreen. They form a transversal pattern with any line that crosses the screen.
3. Staircase with railing

Staircases are designed with a rail that you hold to support yourself. The rail is supported by posts and spindles.
If you imagine a line running in across the middle of the spindles and posts, they form transversals
4. Tie stripes patterns

Many ties are patterned with parallel lines that crisscross each other to give a trendy appearance.
Any of these lines would form transversals since they cut other parallel lines
5. Road intersections

In order to allow smooth traffic flow from multiple directions and prevent jams, roads can be made with intersections such as intersecting streets.
This can form transversals when two or more parallel streets are intersected by a third street.
6. Pineapple skin

The patterns of a pineapple surface have lines running across it. Those from transversals as they cut into parallel lines at diagonal angles
7. Tennis ball nets

A rectangular net helps divide the two halves of a tennis court to keep them separate.
Its braided cord material forms a mesh for blocking the ball from passing through it. The mesh has crisscrossing lines that form transversals.
8. Railway crossing

Railways and roads frequently intercross one another. If a road cuts through 2 parallel tracks of a railway, the result is a transversal.
9. Fencing

Many fence materials are made with intersecting wires or wooden structures. This may form transversals when some wires cross two or more parallel wires.
Conclusion
Understanding transversals is critical as it enables us to solve many common problems we meet in geometry.
If we can identify key angle relationships produced by a transverse line, it is easy to find unknown or missing angles.