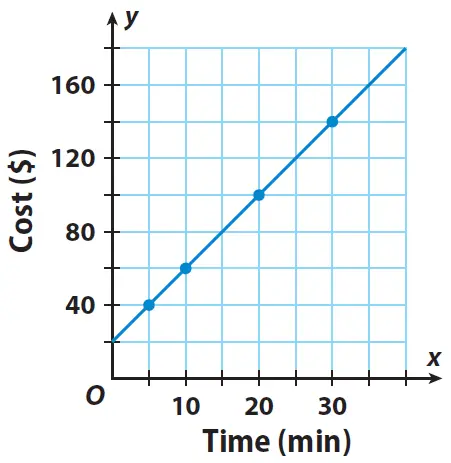
Linear relationships describe a direct correlation between two variables, wherein a change in one variable results in a proportional change in the other, following a straight-line pattern on a graph.
Whenever you have a constant rate change, this gives a linear relationship.
Essentially, this is a relationship where one variable changes at a constant rate in relation to the other.
A linear relationship will always produce a straight line when graphed.
Since it has two variables, it has two dimensions which are represented by the x-axis and y-axis.
In this way, it compares the rate at which one variable changes against the other.
How to Depict A Linear Relationship
This can be done in two ways:
A. As a straight line on a graph:
This results in a line with a constant (fixed) slope.
It differs from other relationships (called polynomials or nonlinear relationships) which usually have curves with variable slopes.
B. As a mathematical equation:
For this, we use the general equation for all linear relationships:
y= mx + b
where
- y stands for the dependent variable y
- x is the independent variable
- m is a constant number which is the slope of the line
- b is the value (a constant) where the line cuts the y axis
The Slope gives the Rate of change
You can always know the rate of change of a linear relationship from the slope of its line.
In addition, the slope gives you other information like:
- The steeper your line, the greater the slope which means the higher the rate of change
- If the line is positively sloped, this means the two variables (x and y) are positively related. When x increases, y increases.
- If the line is negatively sloped, the variables are negatively related. When x increases, y decreases.
Let’s explore examples of linear relationships in real life:
1. Constant speed

If a car is moving at a constant speed, this produces a linear relationship.
For example, a car moving constantly at 50 km/ hour doesn’t change the rate at which it is moving. With each hour, its speed remains fixed
2. Sales

If you have a coffee shop, you can relate the sales you make with the number of sandwiches you sell.
This produces a linear relationship expressed in the following way:
Sales = price x sandwiches sold
y=2x which is a linear equation
where y = sales in dollars and x = sandwiches sold.
2 is the constant value that stands for the price of one sandwich
3. Voltage in a Circuit
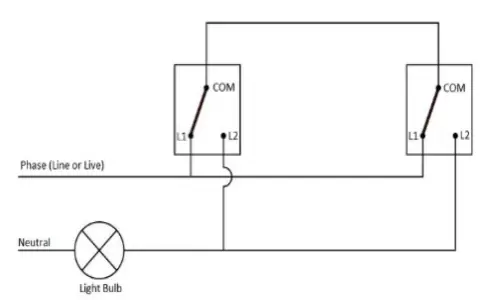
Ohm’s law is a useful function that can be used to relate the voltage and current of a circuit.
It states that these two variables are directly proportional to each other.
This means if voltage doubles, current also doubles. This gives a linear relationship with a constant resistance as shown below (where resistance R is chosen as 200).
y=200x where y = voltage
x=current
200 is a constant value that stands for resistance. It is a property of a particular conductor.
4. Celsius to Fahrenheit

Linear relationships can help us convert from one unit of measurement to another.
For example, the formula that relates Fahrenheit and Celsius is:
C=5/9(F-32)
This can be expanded to:
C=5/9F – (5×32)/9.
The form of this equation conforms to the general linear equation y=mx +b that defines a linear relationship.
It can be written as
y=5/9x – 160/9
Where y is the temperature in Celsius
X is the temperature in Fahrenheit
-160/9 is the value of y where the line cuts the y axis
5/9 is the slope of the line
5. Taxi Fare

The fare that a taxi charges you can be shown to have a linear relationship with the miles covered for your journey.
Here is an example where the price is fifty dollars for every mile traveled.
y=50x
Where y is your fare and x is the miles
6. Car Gas Mileage

Gas mileage shows the distance that a specific car can cover on a given amount of gasoline.
This relationship can be modeled through a linear equation that relates gas mileage and your distance traveled.
7. Distance Traveled

If your speed is 40km per hour, we can show a linear relationship between the hours you travel and the distance you travel. This can be expressed as
y=40x
where y is your distance and x is the hours you have traveled
8. Circumference of a circle
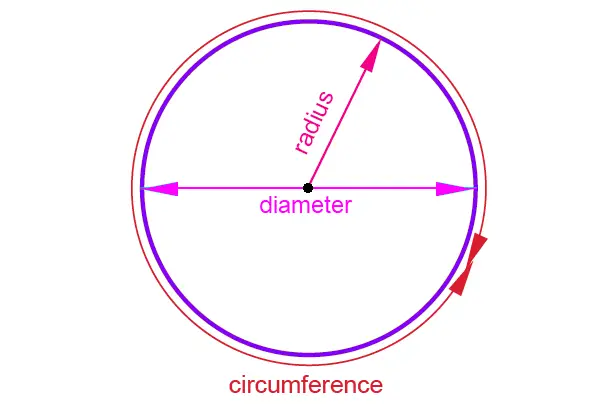
The formula of the circumference of a circle is
C= 22/7(D)
This shows a linear relationship between the circumference and the diameter.
Conclusion
Our world is filled with linear relationships. In this section, we have seen how linear relationships richly add to our knowledge in mathematics, science, and everyday life.