Similarity statements are logical arguments that show how two or more shapes are similar. They focus on two things: the lengths of the sides and angle measures in the two shapes.
The similarity comes from the fact that two figures are identical in shape but differ in size. This is due to a scale factor or scale of magnification that causes contraction, compression, dilation, or expansion.
You can think of this as figures being transformed (shrunk or expanded) from one to the other with the angles being preserved while the distances are changed using the same ratio.
For two shapes to be similar, the ratios relating to their corresponding sides should be the same.
Before proceeding to show similarity, we should be certain about what the corresponding sides or angles of the two figures are.
This ensures that you correctly locate the sides and angles even if the two shapes are not oriented or arranged in the same way in the diagrams.
Corresponding angles and sides lie in the same location as the shapes you are comparing.
Congruence vs Similarity
Congruent shapes are not similar since they have both the exact shape and size.
Similar shapes have the same shape but not the same size.
We use the symbol “∼” to denote similarity. But we use “≅” to denote congruence.
How do you write a Proof of Similarity?
A proof of similarity is a group of statements that give a logical step-by-step explanation or reasons why two figures are similar.
We begin the proof with the initial information that was already given. Then we follow with more statements which end with a conclusion that confirms our proof.
In these proofs, we use evidence and geometric theorems to prove that the figures are similar.
The format of the proofs can take various forms such as paragraphs or flow charts.
However, the most commonly used form is the two-column proof. This is where we organize and present our proof in two columns.
The first column contains the list of statements/conclusions while the second has the reasons supporting each statement.
For example, given two triangles ABC and EDF with their lengths AB=12, AC=18, BC=15 and DE=4, DF=6, EF=5, how can we prove that they are similar?
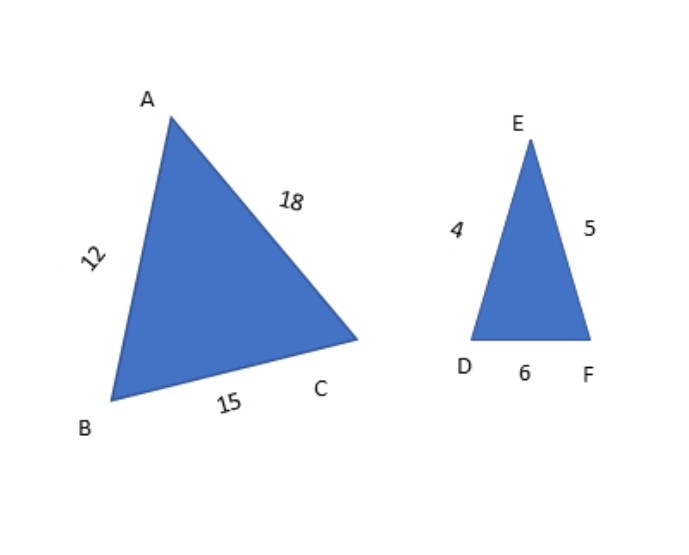
The columns below give a summary of the proof.
On our left-hand side, we give the statements which are numbered to follow the flow of the argument. The right hand has the explanations of each statement. The final statement is the conclusion that states that the triangles are similar.
| Statements | Reasons |
| AB/DE=12/4=3 | Given |
| BC/EF=15/5=3 | 2. Given |
| Angle B=angle D | 3. Given |
| ABC ∼ EDF | From SS theorem |
How do you write a similarity statement for AA?
AA or Angle-Angle is one of the 3 theorems used for proving the similarity of triangles.
By the AA theorem, two triangles can be proved to be similar if two of their corresponding angles are equal or congruent.
The beauty about the theorem is that you won’t have to check all the 3 sides or angles of each triangle for similarity.
Just showing the congruence of two corresponding angles of the two triangles is enough to conclude that they are similar.
This follows from the fact that the triangle angles add up to 180 degrees.
Therefore, if two angles of a pair of triangles are congruent, then their third corresponding angles must be congruent also.
For example, consider the following two triangles ABC and XYZ:
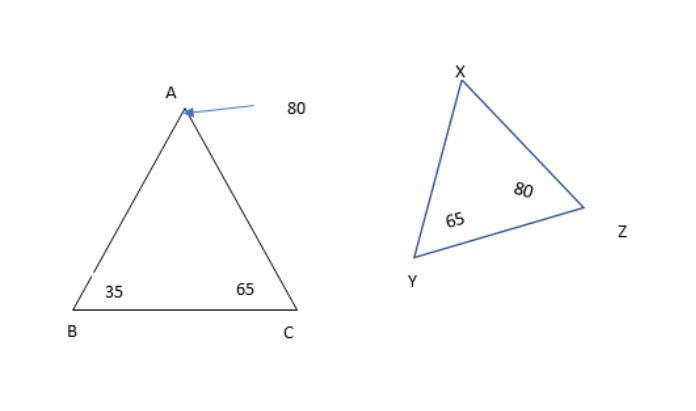
Angle B = angle X = 35°
Angle C=Angle Y = 65°
Since we already have a pair of corresponding congruent angles, by the AA theorem, it follows that:
Angle A = angle X from the triangle sum theorem.
So even without calculating angle X, we can conclude that it is 80° from its congruence with angle A.
This angle can also be calculated as 180° – (65° +35°) = 80°
Therefore, we can conclude that the two triangles are similar or ΔABC∼ ΔXYZ
How do you write a Similarity Statement for a Right triangle?
If ΔABC and ΔXYZ are right-angled triangles and angles.
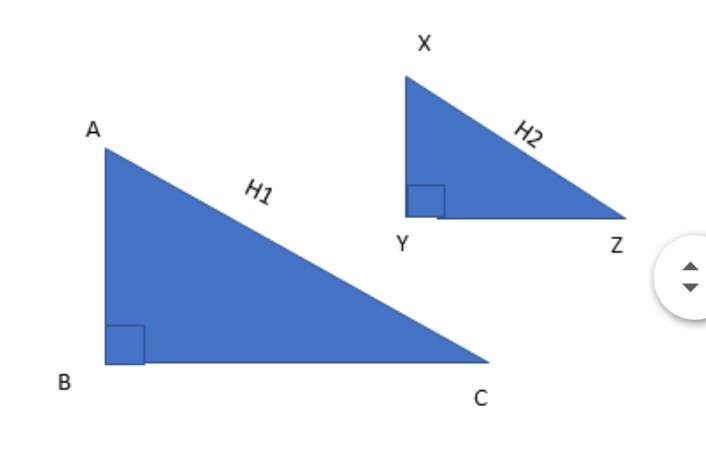
Right triangles have three properties: they each have an angle of 90 degrees, two acute angles (angles measuring less than 90 degrees), and a hypotenuse (H1 and H2).
They also have two shorter sides called the legs.
Related Post: Examples of Right Triangles in Real Life
We can use these properties to write a similarity statement using the three theorems of Acute Angle- similarity, Leg-Leg similarity, and Hypotenuse-Leg similarity.
A. Acute Angle Similarity
By the Angle-Angle similarity we can show that the two triangles are similar if they have a pair of acute angles that are congruent.
In the figure, ∠B≅∠Y, (being both right angles), and ∠A≅∠X.
From this, we conclude that ABC and XYZ are similar or ΔABC∼ΔXYZ.
B. Leg-leg similarity
Using the Side-Angle-Side Theorem, we can prove similarity if the corresponding legs of the two triangles are proportional in their lengths.
Therefore, if our figure shows that AB/XY=BC/TZ, we can conclude that ΔABC is similar to ΔXYZ or ΔABC∼ΔXYZ.
C. Hypotenuse leg similarity
Finally, we can also prove similarity if the hypotenuse and a leg of each triangle are proportional in length to the other.
Since in our figure, H1/H2=AB/XY we can conclude that ΔABC∼ΔXYZ.
How do you write a Similarity statement for a Polygon?
Polygons are any plane closed shapes that are drawn using straight lines as opposed to curves.
Similar polygons have the same number of sides and vertices. They also have equal corresponding angles, and corresponding sides that are proportional to each other.
For any two polygons having the same number of sides (n), if we can show that n-1 of their corresponding angles are congruent, then their remaining pair of corresponding angles are also congruent.
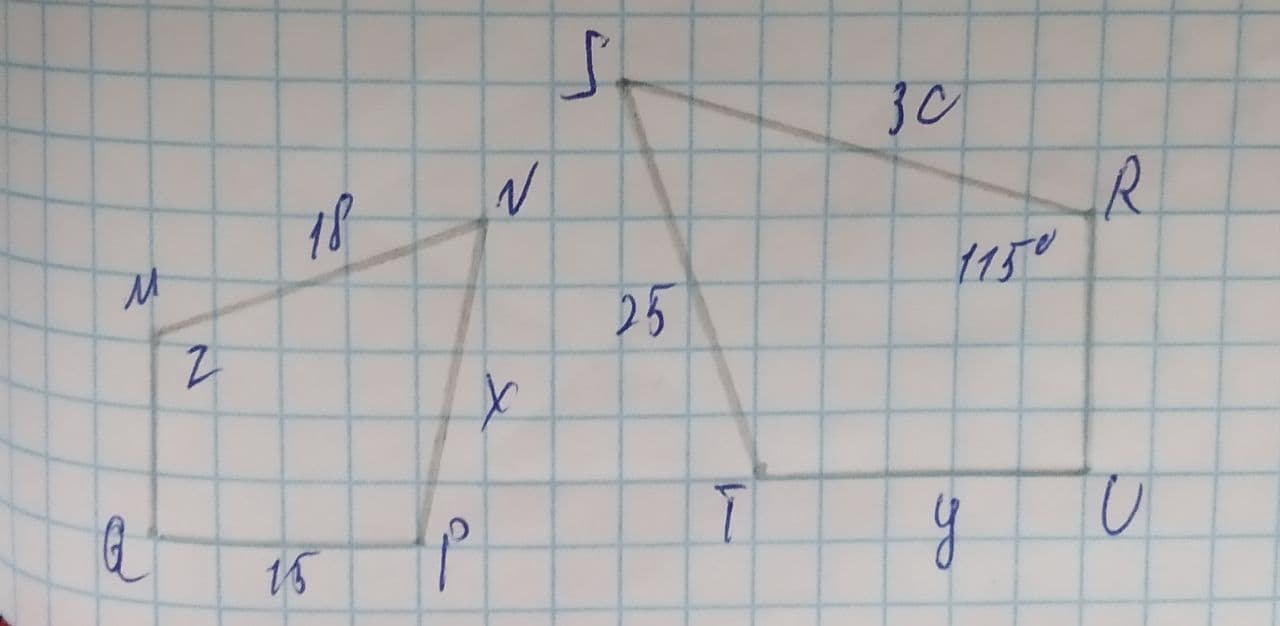
For example, let us compare the two pentagons ABCDE and OPQST.
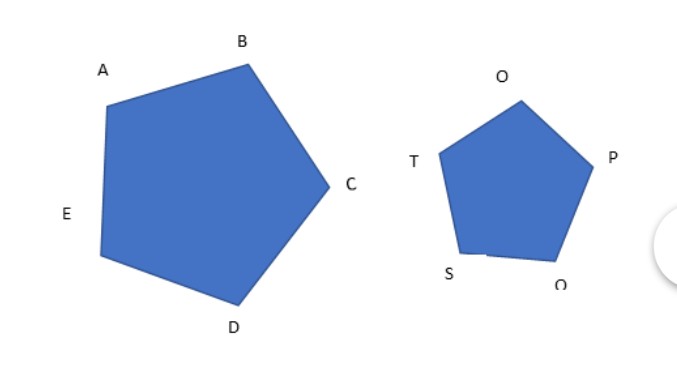
Both have five (i.e.,n) sides, angles, and vertices. If 4 (i.e. n-1) of their corresponding angles are congruent so that;
Angle A = angle T
Angle B =angle O
Angle C = angle P
Angle D= Angle Q:
We can conclude that the remaining pair of corresponding angles E and S are also congruent.
Or Angle E = Angle S
Thus, the two pentagons ABCDE and OPQRS are similar.
In addition to this, another proof of similarity follows that their corresponding sides are proportional to each other by a common ratio k:
AB/TO = BC/OP=CD/PQ=CD/PO=DE/ST= k
Conclusion
Just like we have identical twins, lookalikes, imposters, and disguises among people, mathematics is also filled with these fascinating characters.
And just like the way detectives use DNA, fingerprints, and hair samples to determine close relatives or to catch criminals, mathematics uses tools like theorems, definitions, properties, postulates, and logical proofs to determine objects that are similar to each other.
Image source: 1, 2, 3