An equation is any algebraic expression that has two parts set up to be equal to each other through an equal sign. Examples are:
x + 4=10
x + 5=y
There are many kinds of equations but linear equations are the simplest and most common ones.
It is a special type of equation that contains only one or two variables/ unknowns which are of degree one. This means its variables (x, y, etc) are expressed only in powers of one.
For an equation to be a linear equation, it should satisfy the following:
- Contain only one or two variables (not 3 or more)
- A variable should never appear in a fraction as a denominator (e.g 6/x)
- If it has two variables, they should not appear together as a single term (i.e multiplied to each other such as xy)
- No variable should have a power or exponent of more than 1 (eg it can’t have x^2 or x^4)
(Note that although it is not usually indicated or written, the term “x” has a power of one; i.e x and x^1 are the same term)
Look at the following examples to identify a linear equation.
- x^2 + 6x = 2 (not a linear equation because it contains x^2 which makes x a power of two)
- x^3 + 7x = 5 (not a linear equation because it contains x^3 which makes x a power of 3)
- 5xy +2x=4y (not a linear equation because it has the term 5xy in which two variables x and y appear together in the same term)
- 1/x +5x=8 (not a linear equation because x appears in 1/x as the denominator of a fraction)
On the other hand, look at these examples:
- x+ 5=15 (linear equation )
- x + 3y= 10 ( linear equation because it has only 2 variables, x, and y which are all powers of one)
- 2/x +5=4 (although x appears as a denominator in the fraction “2/x” this is still a linear equation. This is because when you simplify it by multiplying each side with x it becomes “2 +5x=4x” where the x disappears from the denominator)
The term linear comes from the word line. But what do linear equations have to do with lines?
It’s because when you plot linear equations on a coordinate plane, they produce a straight line.
Other types of equations which are non-linear produce non-linear graphs such as curves.
Solving Equations
Equations will always contain a term whose value is unknown.
Solving an equation means finding what the values of those unknowns are.
To do this, you need to isolate the variables so that they appear alone on one side of the equal sign.
All the other elements (i.e numbers) should appear on the opposite side of the equal sign.
Here are 10 examples of linear equations in real life:
1. Number Problems

I think of two numbers. The larger of them is 3 times larger than the smaller. If I increase the larger number by 10, the result will be 5 times the small number. What are the numbers?
Solution:
If the smaller number is x then the big number is 3x.
Create your equation:
3x +10=5x
Subtract 3x from both sides so that all x terms appear on one side (RHS)
3x-3x +10=5x – 3x 10=2x
Divide both sides by 2 to get:
5=x
The 2 numbers are 5 and 5×3=15
2. Speed, Time, and Distance Problem

A car travels from town A to town B in 6 hours and covers 720 km. What is its speed?
Solution:
We use the formula speed=distance/time
Or s=d/t
Our known values are d=720 and t=6
Create the equation:
s=720/6
s=120
Therefore the speed is 120 km/h
3. Age Problems

If Dominic is 36 years older than Peter and was twice Peter’s age 8 years ago, how old are their ages now?
Solution:
Let x = Peter’s age now
Then
x+36 = Dominic’s age now
8 years ago, their ages were:
Peter: x-8
Dominic: (x+36)-8
Create the equation and solve:
(x+36) -8 = 2(x-8)
expand both brackets to get:
x+ 28=2x-16
Add 16 on both sides to get:
x+28+16=2x-16+16
x+44=2x
Subtract x from both sides to get:
x-x+44=2x-x
44=x (Peter’s age now)
x+ 36= 44 +36 = 80 (Dominic’s age now)
4. Money and Percentage Problems

A seller sells a calculator for $78. 50 after a markup of 15%. (the markup is the amount the seller adds to a good’s cost to enable him to make his profit). How much did the seller buy the goods from the manufacturer?
Let p be the cost of the calculator.
A markup of 15% means 15% of p was added to the cost (p) to get its seller’s price.
Create equation:
p +(15/100 x p) =78.50
Multiply both sides by 100 to get:
100p +15p =7850
115p=7850
Divide both sides by 115 to get:
p=7850/115
p=$68.26
5. Wage and Hourly Rate Problems

Company A offers to pay you $450 per week. It requires you to work. What is its hourly pay?
Create equation:
450=40x
Divide both sides by 40.
11.25=x
Ans: rate is $11.25 per hour.
6. Geometry Problems
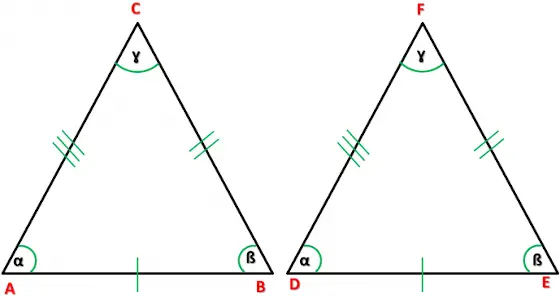
Use a linear equation to find out the angles of an equilateral triangle.
An equilateral triangle is a triangle with all three sides and angles equal.
If one angle is x, create your equation:
x + x + x = 180
3x=180
x=60
Therefore each angle is 60 degrees.
Related Posts:
Real-life Examples of a Ray in Geometry
10 Real-Life Examples of a Plane in Geometry
7. Consecutive integer problems

Find three consecutive odd integers whose sum is 33.
You can represent the consecutive odd integers as x, x+2, x+4
Add these and create your equation then solve:
x + (x+2)+(x+4)=33
3x+6=33
3x=33-6
3x=27
x=9
Therefore the integers are 9, 11, and 13
8. Coin Mixture problems

James has 24 coins in nickels and quarters. In total, he has $3.00. How many nickels and quarters does he have?
If n is the number of nickels
25-n = number of quarters
0.25n = money from nickels
0.05(25-n)=money from quarters
Create your equation:
0.25n + 0.05(24-n)=3
Solve:
0.25n +1.2 – 0.05n=3
0.2n+1.2=3
0.2n=1.8
n=9
The number of nickels was 9 and quarters was (25 – 9) =16
9. Fraction Problems
A girl is ¼ of her dad’s age currently. After 5 years, she becomes ⅓ of her father’s age. What are their ages now?
Let x be the father’s current age.
Give both of their ages in terms of x:
Father:x
Daughter: ¼ x
After 5 years their ages are:
Father: x +5
Daughter: ¼ x +5
The daughter’s age was also ⅓ of dad’s age.
Create an equation from this and evaluate:
1/4x +5 =⅓(x+5)
Open brackets on RHS
1/4x +5 =1/3x +5/3
Subtract 1/3x from both sides
1/4x-1/3x +5=5/3
Subtract 5 from both sides
1/4x-1/3x=5/3-5
Evaluate both sides:
-1/12x=-10/3
x=40
Father’s age:40
Girl’s age:10
10. Getting the Slope of a Line

Given any linear equations, you can know its slope and y-intercept when you graph it on a coordinate plane.
To know this, you should arrange its terms to be in the form:
y=mx+c
- where y =y variable which is the dependent variable
- m=slope of the line
- x= independent x variable
- c=value of y where the line intercepts the y axis.
For example, if your equation is 6x +y =5
Rearrange it to make y appear alone on one side.
6x +y=5
Subtract 6x from both sides:
6x-6x+y=5-6x
y=5-6x
Rearrange further to correspond to y=mx +c
y=-6x+5
So at a glance, this equation tells you that its slope is – 6 and it intercepts the y-axis at 5.
Slope is a vital piece of information that tells the rate at which y changes in relation to x. The y-intercept value shows you the value of y when x is zero.
Conclusion
Linear equations are the most basic equations in mathematics. They have wide relevance in ordinary life and research in solving problems.
Related Post: 12 Examples of Linear Regression in Real Life