An angle is one of the fundamental aspects of geometry, and it plays a crucial role in shaping the world around us. Corresponding angles, in particular, are a critical concept in geometry that can help us understand how different objects interact.
What are Corresponding Angles?
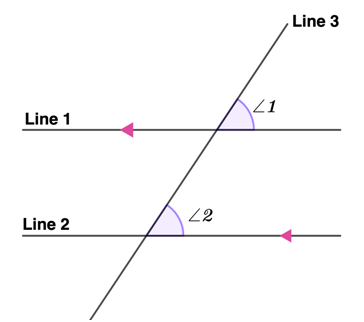
Corresponding angles are formed when a third line, known as a transversal, intersects two parallel lines.
Corresponding angles are always congruent. In other words, if two angles correspond, they will be the same size and measure. They are in the same position relative to the parallel and transversal lines.
For example, if one corresponding angle is on the top right side of a transversal, the other corresponding angle will also be on the top right side of the transversal.
If two corresponding angles are congruent, then the lines they are on must be parallel.
15 Real-Life Examples of Corresponding Angles That You Can Find Around You
1. Ladders
When a ladder is placed against a wall, it forms corresponding angles at the point where it touches the ground and the wall. These two angles are called corresponding angles because they match each other in size. This helps ensure your ladder is at the right angle so you can climb up safely!
2. Ceiling tiles
Ceiling tiles have edges and corners that form angles. If two tiles meet at an intersection, they create a 90-degree angle. The shape of the tile can determine what kind of angles will be made when installed on the ceiling. Regardless, the tiles join together to create corresponding angles, thus creating neat lines in your ceiling.
3. Doorways
Have you ever noticed that the hinges on a door are at an angle? Those angles correspond with the angles of the door frame. The top hinge creates one angle, and the bottom hinge creates another angle that matches up with the angles of the door itself. This helps keep everything aligned properly so the door can open and close smoothly without getting stuck or jammed.
4. Window frames
Window frames have horizontal and vertical bars, creating angles where they meet. These angles match each other, meaning that if you draw lines from the ends of one angle to the corresponding ends of another, they will form straight lines. This helps keep the window frame sturdy and secure.
5. Skyscrapers
When you look at a skyscraper, you might notice that the corners of the building create angles that match each other. For example, if one corner has an angle of 90 degrees, the opposite corner will also have an angle of 90 degrees.
Also check:
10 Examples of Obtuse Angles in Real Life
8 Real-Life Examples of Supplementary Angles
6. Power lines
Power lines are built at specific angles. When you look at a power line tower, it will have corresponding angles with its cables. This means that if the tower leans in one direction, then the cable attached to it will also lean in that same direction.
7. Garden fence
A garden fence usually consists of posts, which are vertical supports, and rails, which are horizontal bars that connect the posts. They ensure that the fence is properly aligned and stable.
8. Staircases
The angle formed by each step and the ground matches the angle on the other side, making it easier for people to climb up or down without tripping or falling. Studies show that if you climb stairs with uneven steps, you may find it challenging to maintain your balance. However, when each step has a matching angle on both sides, it creates an even surface that is much safer and more comfortable for people.
9. Rubik’s cube
A Rubik’s cube consists of different colored squares on each side. The sides and corners of the cube can be moved around to create different patterns. When you look at the angles formed by the sides and corners, they match up in a certain way. This means that if you rotate one side or corner, it will also affect the angles of other sides or intersections.
10. Chess Boards
The diagonal lines on the chessboard go from one corner to another that is not adjacent. These diagonal lines form corresponding angles, which means that if you draw a line through each angle, those two lines will be equal in length and opposite in direction.
11. Hand fans
Hand fans consist of multiple segments that can be folded or unfolded. When you fold the segments together, they create an angle between them. Similarly, when you spread the segments, they make an angle between them. These corresponding angles match each other depending on how you manipulate them.
12. Lawnmowers
The blades of a lawn mower are the sharp parts that spin around and cut the grass. When these blades cut, they make angles with the ground. These angles match each other, so if one blade is at a certain angle, all the other blades will also be at that same angle. This helps to ensure that all parts of your lawn get cut evenly, without any patches being missed or left longer than others.
13. Railroad tracks
The rails on a railroad track are placed at a specific angle to each other. These angles are always equal and opposite to each other. So, if one rail is angled in one direction, the other will be angled in the opposite direction. This helps keep trains on track and prevents them from derailing or going off course.
14. Bookshelf
Bookshelves usually consist of shelves supported by vertical sides or panels. The angles created by the shelves and bookshelves’ sides can correspond, meaning that the angle at which one frame meets a side panel will match the angle at which another shelf meets the same panel. This creates a uniform look for the bookshelf and makes it more aesthetically pleasing.
15. Rulers
A ruler usually has measurement marks that show how long or wide something is. If you place the ruler flat against an object and look at it from the side, you will see that each mark lines up with a certain angle. These angles help ensure your measurements are accurate and consistent every time you use the ruler.
Related Posts: